
ZULF NMR: The search for elusive spin-spin interactions
The Secular Approximation
Interesting applications of ZULF NMR arise from the fact that spin evolution and its detection happens in a spherically symmetric magnetic environment. Interactions that nuclear spins experience can be divided into two groups: external interactions with external magnetic fields and internal interactions with local magnetic fields. External interactions include the interactions with the imposed permanent or pulsed magnetic fields, as well as radiofrequency pulses in the case of high-field NMR. These interactions are usually much larger than the internal ones and they break the spherical symmetry of the magnetic environment (Figure 1). The internal interactions include various interactions of a spin with local magnetic fields and with other spins. The most important internal interactions are: chemical shift – the interaction of a spin with the local magnetic field of its environment, influenced by electron distribution; spin-spin indirect J-coupling – the interaction between two nuclear spins that is conducted through electrons constituting chemical bonds; direct dipolar spin-spin coupling of two nuclei spins, and others. A unique feature of ZULF NMR is that at low fields the internal interactions are not truncated by external fields, and most terms of the internal spin Hamiltonian can be easily observed as a coherent evolution of the spin ensemble. This provides additional information that is difficult extract from high-field NMR.
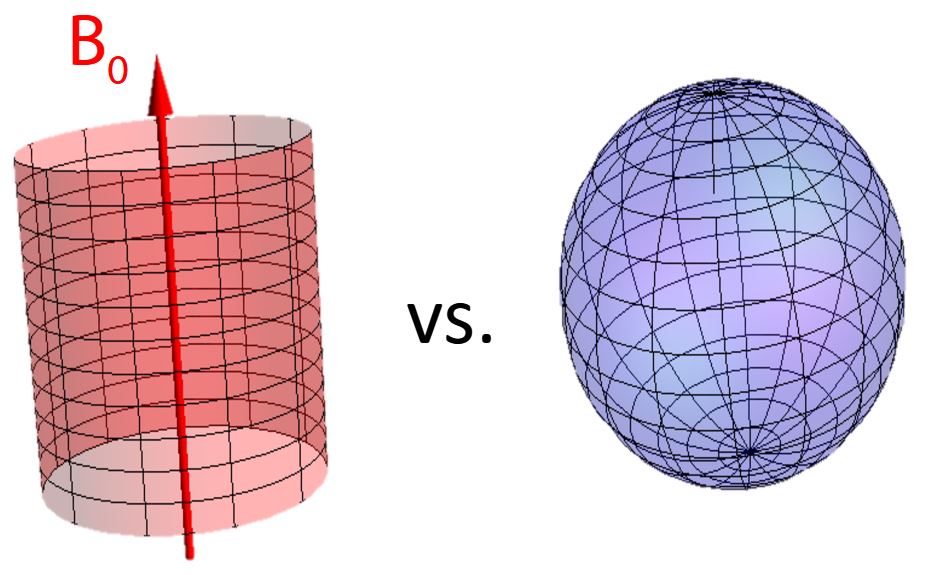
Figure 1: Comparison of the symmetry of the external magnetic field surrounding a molecule in high-field and ZULF NMR. The uniaxial symmetry is imposed by the strong magnetic field in case of high-field NMR, whereas spherical symmetry of the magnetic environment is conserved in ZULF NMR experiments.
Let us analyze in more detail which internal interactions disappear at high field. The dominant interaction in high-field NMR is always the interaction of a nuclear spin with the main magnetic field, B0, the Zeeman interaction. The applied B0 field usually lies in the range of 1-20 T and it induces Larmor precession of the nuclear spins. The frequencies of the Larmor precession are of order of 108 Hz and they are always significantly larger than frequencies characterizing internal spin interactions (excluding perhaps the quadrupolar interaction which is not considered here). In such a situation, only the terms of the spin Hamiltonian that commute with the Zeeman Hamiltonian remain unchanged. However, there are many terms that do not commute, which means they essentially vanish. The eigenbasis of the spin Hamiltonian is determined prediminantly by the large Zeeman term, and so the eigenstates of any spin system placed in high magnetic field are close to Zeeman basis states. Zeeman states are the direct products of the individual basis states, such as spin-up and spin-down states of a spin-1/2 particle. The only important off-diagonal terms of the Hamiltonian (represented in the Zeeman basis) are those whose amplitudes are comparable to the difference between the corresponding diagonal elements of the Zeeman operator. All other off-diagonal elements are washed out and do not contribute to the coherent evolution of the spins. Neglecting these off-diagonal terms is called making the secular approximation.
To illustrate this, let us consider a 1H spin J-coupled to a 13C spin. Matrix plot representations of the Hamiltonian for this spin pair in a 10 T and 10 nT magnetic field are shown in Figure 2. The Hamiltonian appears as a diagonal matrix in high-field case. This is a well-known example of a weakly coupled spin pair, and it is valid when the difference between the Larmor frequencies is significantly larger than the J-coupling. This is always true for nuclei of different species in `conventional' NMR, because the difference in Larmor frequencies is huge. Secularization of the Hamiltonian leaves only the spin operators parallel to the B0 field and removes all the orthogonal components from the original J-coupling Hamiltonian. This can be written using product operators: \[\hat H_J = J \hat I \cdot \hat S,\] \[\hat H^{sec}_J = J \hat I_z \cdot \hat S_z,\]
Here \(\hat I\)and \(\hat S\) are the vector spin operators of the interacting spins,and \(\hat I_z\), \(\hat S_z\) are their projections on the z-axis (which is selected to be along the B0 field). \(J\) is the isotropic part of the J-coupling constant.
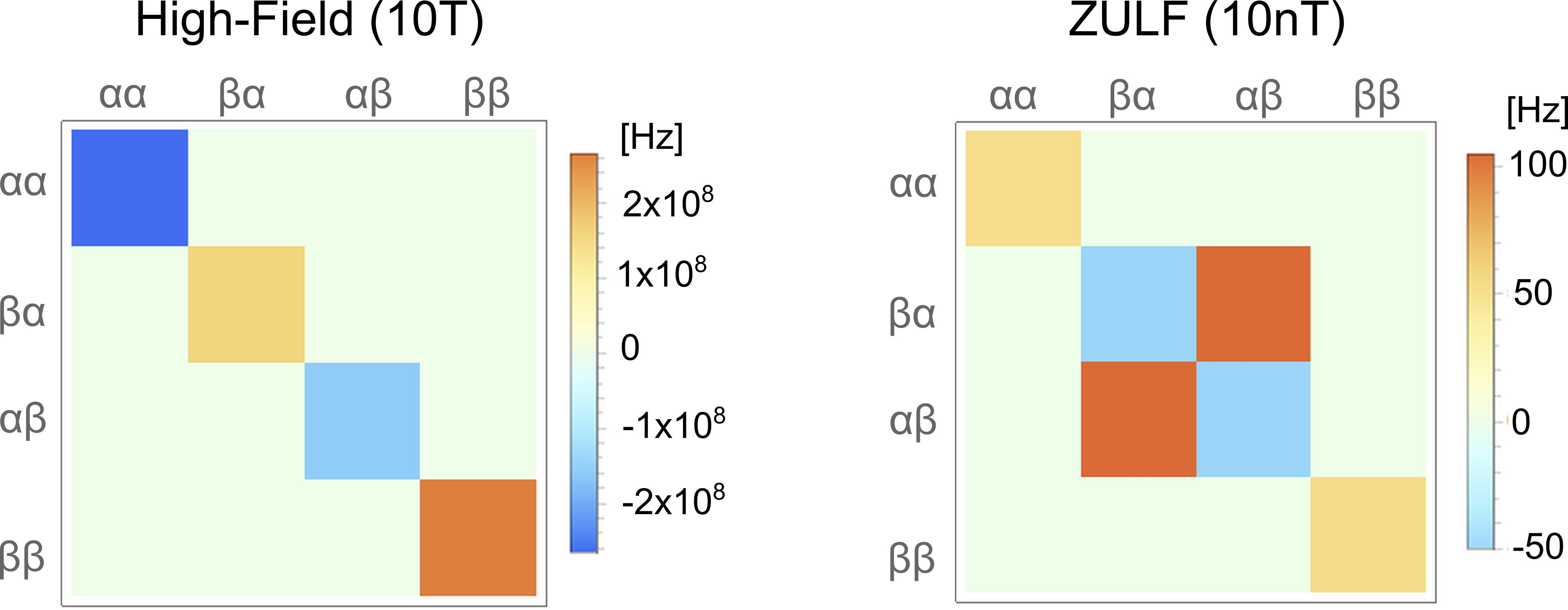
Figure 2: Matrix plot representation of the Hamiltonian of a 1H-13C pair with a J-coupling of 210 Hz in an external magnetic field of 10 T (left), and 10 nT (right).
However, this secularization is not valid in the ZULF regime, where the non-secular terms become larger than the Zeeman terms. This can be seen in Figure 2 for the ZULF case: the largest elements in the Hamiltonian are the off-diagonal matrix elements. Consequently, the secular approximation is not valid and the 1H-13C spins appear to be strongly coupled in the ZULF regime (e.g., J-couplings are much larger than differences in Larmor frequencies). The eigenbasis also changes: for the spin pair it becomes close to the singlet-triplet basis.
Thus, the spin Hamiltonian in the ZULF regime is not truncated by the imposed symmetry of a large external magnetic field and most non-secular terms in the high-field case can be easily observed as a coherent evolution of the nuclear spins. For illustration, we will again consider the coupled pair of 1H-13C spins. The thermal-equilibrium state of this spin system at high field corresponds to a state in which 1H spins are polarized along the B0 field about 4 times more strongly, than the 13C spins. This state does not evolve with time, as can be seen in Figure 3. However, if this state is created at zero to ultralow field, it starts to evolve, as can be seen from the ZULF case in Figure 3. The original 1H polarization coherently transfers to the 13C spins, while the original 13C polarization transfers to 1H spins. The oscillation happens with the J-coupling frequency (210 Hz in our example), and this gives rise to the J-spectra in ZULF NMR.
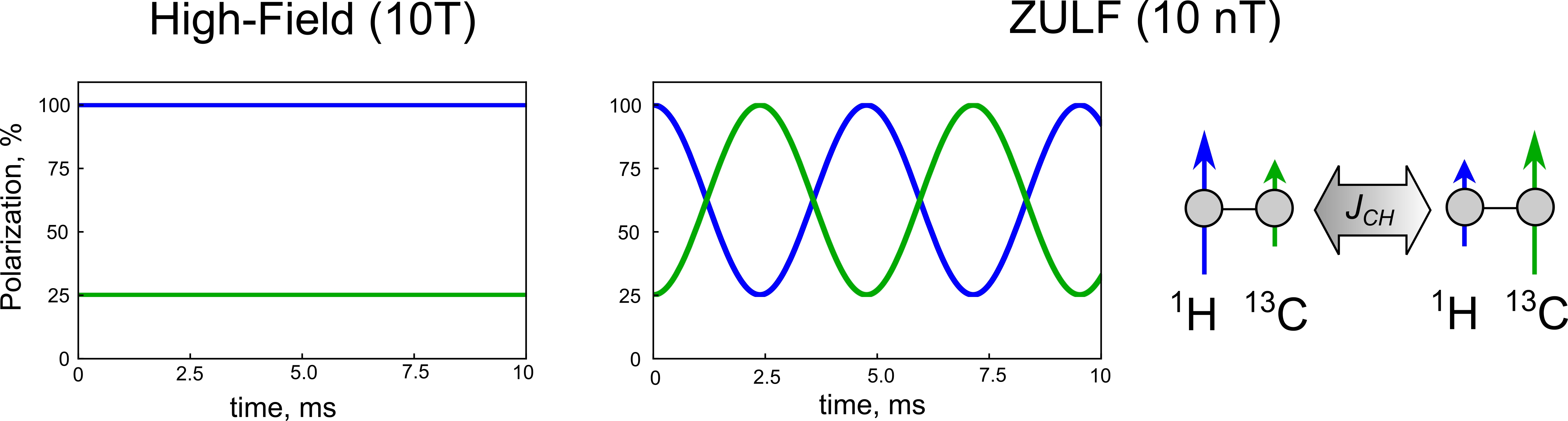
Figure 3: Evolution of Zeeman polarization of two J-coupled spins. In high field the coupled 1H-13C spins do not evolve under the non-secular J-coupling terms. This state does evolve at zero or ultralow field: polarization of the two coupled spins is coherently exchanged with the frequency of the J-coupling (210 Hz).
However, we would like to note that in high-field NMR it is still possible sometimes to initiate coherent spin evolution under non-secular terms, although it is more complicated. Such experiments might, for example, require the use of additional spin-locking fields that reproduce conditions reminiscent to those at zero-field.
Antisymmetric J-coupling
One particularly interesting type of spin-spin interaction is the antisymmetric part of the J-coupling tensor. The existence of the antisymmetric J-coupling was suggested almost four decades ago [1], and since then many quantum chemical calculations confirmed the existence of this interaction [2]. However, to date it has never been observed experimentally. Let us delve deeper into the J-coupling to better understand this interaction and what is meant by the antisymmetric part.
Usually when we talk about molecular J-couplings we refer to the isotropic part, because this is the relevant part for molecules tumbling rapidly in solution. However, the interaction depends on molecular orientation and it is a tensor quantity. The J-coupling interaction Hamiltonian for two spins may be written: \[\hat H^{full}_J = \hat I \cdot J \cdot \hat S\]
It is convenient to group the terms of the tensor \(J\) according to their transformation properties under 3D rotations: \[J = J^{(0)} + J^{(1)} + J^{(2)}\] The first term, \(J^{(0)}\), is the isotropic part of the J-coupling; it does not depend on molecular orientation, so transforms as a scalar quantity or a zero-rank tensor under rotations. \(J^{(0)}\) is the part that is commonly-observed in solution-state NMR experiments. The \(J^{(1)}\) and \(J^{(2)}\) components, on the other hand, do depend on the molecular orientation, and for solution-state NMR they are averaged out due to fast molecular tumbling. In order to observe them, one should restrict isotropic reorientation of the molecules. The \(J^{(1)}\) component transforms as a vector upon rotations, corresponding to a first rank tensor, whereas the \(J^{(2)}\) component transforms as a second rank tensor. Let us consider the properties of \(J^{(1)}\) in more details. It can be represented as 3x3 matrix in cartesian coordinates: \[J^{(1)} = \begin{pmatrix}0 & -J_{xy} & -J_{xz}\\J_{xy} & 0 & -J_{yz}\\J_{xz} & J_{yz} & 0\end{pmatrix}\]
As we mentioned, under 3D rotations the 3 independent components \(J_{xy}\), \(J_{xz}\) and \(J_{yz}\) transform as coordinates of a vector. However, something unexpected happens to these components under reflections; they behave as components of a pseudovector. This transformation is illustrated in Figure 4. The \(J_{xz}\) component, which is perpendicular to the mirror plane, is unaffected, whereas the two other components are inverted. Pseudovector quantities are not uncommon physics; magnetic field and angular momentum are good examples. This is illustrated in Figure 4 for the angular momentum of a spinning wheel.
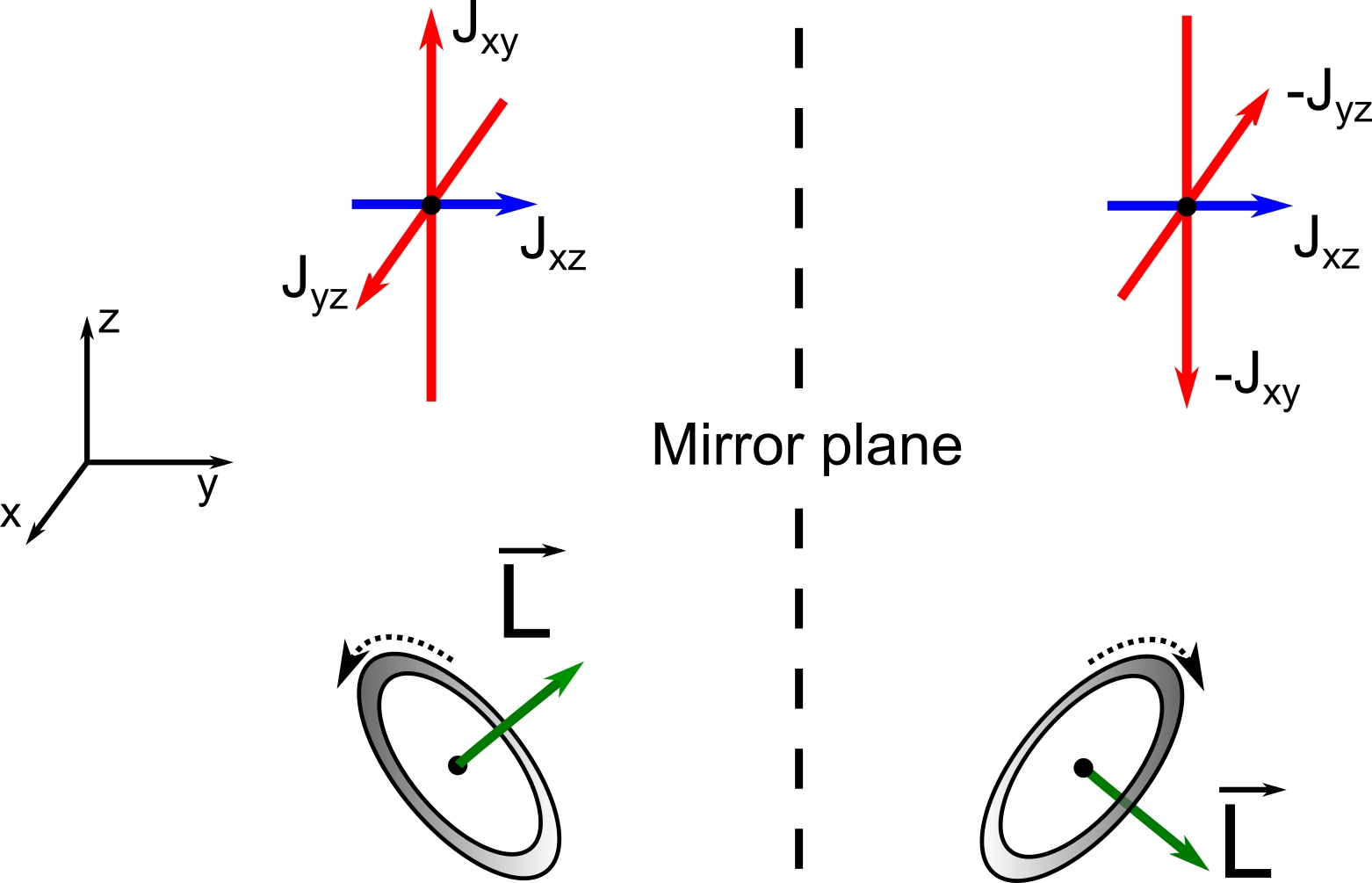
Figure 4: Top: Schematic representation of how the components of the \(J^{(1)}\) tensor are transformed under reflection. The component perpendicular to the reflection axis stays the same, whereas the other components change sign. Such a transformation is that of a pseudovector. This is equivalent to the angular momentum of a spinning wheel (bottom).
Finally, this interaction has another feature that makes it completely different from all other known spin-spin interactions: its Hamiltonian is antisymmetric with respect to permutation of the two coupled spins: \[\hat H^{anti} = \hat I \cdot J^{(1)} \cdot \hat S = -\hat S \cdot J^{(1)} \cdot \hat I\] These unique properties of the \(J^{(1)}\) coupling make it possible to use the antisymmetric J-coupling components to distinguish molecular chirality.
Chirality in NMR spectroscopy
A chiral object has two mirror images, which cannot be transformed into each other by a 3D rotation. Molecular chirality is an important property for chemistry and biology. Mirror images of a chiral molecule are called R- and S-enantiomers. Many chemicals, notably amino acids and sugars, exhibit chirality, and it is often of key importance for bioactivity. It is well known that almost all amino acids in organisms are found to be left-handed, while sugars are predominantly right-handed; their left-handed counterparts are not metabolized. Chirality defines chemical reactivity in many organic reactions, making this property important also for organic synthesis.
Despite being such an important property, chirality is difficult to probe with spectroscopy. For instance, left-handed and right-handed molecules produce the same NMR spectra. This is because all the internal interactions commonly observed in NMR spectroscopy, isotropic and non-isotropic, are identical for a molecule and its mirror image. This is however not true for the antisymmetric J-coupling, as was shown in the previous section.
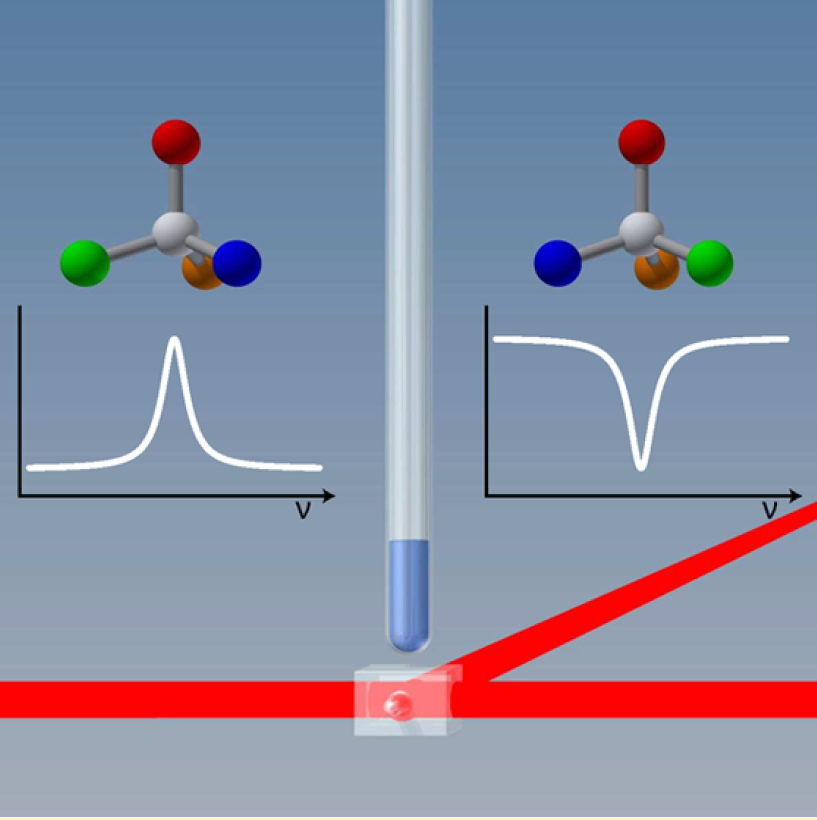
Figure 5: Illustration of a proposed ZULF NMR experiment to detect the antisymmetric J-coupling. R- and S-enantiomers will produce spectra with opposite phases, since the two enantiomers have different antisymmetric J-coupling tensors. The figure is taken from Ref. [3].
The peculiar property of the \(J^{(1)}\)-coupling to transform as a pseudovector has led to the development of experiments that would potentially enable distinguishing enantiomers of a chiral molecule directly from NMR spectra. All these approaches suggest orienting molecules in order to prevent \(J^{(1)}\) being averaged by molecular tumbling in solution. ZULF NMR is a particularly promising approach as it allows directly detecting \(J^{(1)}\) between heteronuclear spins. Figure 5 illustrates that oriented R- and S-enantiomers would produce ZULF NMR spectra with opposite phases since the two enantiomers have different projection of \(J^{(1)}\) onto the orientation axis. This component drives the coherent spin evolution with opposite signs for the left- and right-handed enantiomers.
The ability to directly distinguish chirality from NMR spectra would be a great development for analytical chemistry. Such experiments would also enable us to study the breaking of fundamental physical symmetries. ZULF NMR has great potential for solving these challenging tasks, since it is easy to detect the non-secular interactions.
Literature references:
- A.D. Buckingham, P. Pyykkö, J.B. Robert, and L. Wiesenfeld, “Symmetry rules for the indirect nuclear spin-spin coupling tensor revisited ” Mol. Phys. 46, 177 (1982)
- P. Garbacz, “Computations of the chirality-sensitive effect induced by an antisymmetric indirect spin–spin coupling” Mol. Phys. 116, 1397 (2018)
- J.P. King, T.F. Sjolander, and J.W. Blanchard, “Antisymmetric couplings enable direct observation of chirality in nuclear magnetic resonance spectroscopy”J. Phys. Chem. Lett. 8, 710 (2017)

 This project has received funding from
the European Union's
This project has received funding from
the European Union's 

















